Ballistics
Ballistics is the physical science that governs how a projectile is fired and how it flies. In a pedantic definition, ballistics is treated as two separate realms: Internal Ballistics, which focuses on how the charge propels a projectile within the bore of a gun and External Ballistics, which focuses on how the projectile flies once it has left the gun. External ballistics is so vastly predominant in its import that one can generally assume when reading mention of "ballistics" that the writer means to refer to external ballistics.
The various naval powers built a considerable scientific and mathematical understanding of ballistics. They applied their understanding to solve a fundamental problem: they needed a complete understanding of a complex system that could not be fully tested.
Constructing an accurate sighting system for a gun requires an accurate understanding of where the shell will fall when fired at different angles of elevation (the means of firing to different ranges) or at different muzzle velocities (the powder might be at the wrong temperature, or the bore of the gun worn out from use) or at atmospheric conditions that vary from a nominal standard (air resistance changes with temperature). The problem is easy to see: there are too many variables to allow complete empirical testing of the gun. The application of the scientific understanding of ballistics became the means by which a few test firings could be massaged into a tabular record of firing data (called a range table) that accurately reflected how the gun would perform under the conditions that were never actually tested. The range table became the data set used in designing the sighting system for a gun that could be accurately fired in any conceivable set of conditions.
Contents
Forces acting upon a shell in flight
The two most powerful forces on a shell are the force of gravity and the aerodynamic drag caused by the shell having to push its way through the air. Gravity is pretty easy to characterize, as it is essentially a constant and always directed downward. Drag is trickier, as it depends upon the shape of the shell and the speed of sound, which varies according to the shell's present location. Secondary factors worth considering are wind and ballistic drift caused by the shell's spiral flight imparted by the rifled gun barrel. Lastly, the Coriolis effect might affect the shooters' perception of the shell's flight, and some relatively minor aerodynamic effects also affect the shell.
Although the scientists of the day were fully capable of computing the effect of most such forces at any given moment -- a feat repeatedly demonstrated in manuals in a morass of the most appalling mishmash of systems of measure where angles are measured in degrees, minutes and seconds, velocities variously in feet per second and knots, etc -- they lacked any means of simulating the accumulated effect of these instantaneous influences over the course of a shell's trajectory.
The approach they took was to learn all they could about an idealized shell type through experimentation, and compiled these findings into O. B. Ballistic Tables (O.B. meant "Ordnance Board"; previously, a different set called "Ingall's Tables" were employed). When proving a new weapon system, they fired enough test shots at various angles of elevation that they could see how the gun differed from this idealized weapon system and then provide a few simple fudge factors ("coefficient of reduction") that allowed the idealized data to be distorted into a description of the new weapon despite having conducted very few test firings. Their ability to do this with high precision is a testament to the strong background they had in mathematics, though even a neophyte such as I gets the idea that some seat-of-the-pants guesstimation was woven into the process.
The Admiralty placed great confidence in these approximations[1], specifying that the range tables outlining the performance of their guns were based on O. B. Ballistic Tables compiled in June, 1903 at Shoeburyness, indicating that discrepancies attributable to the underlying use of Sciacci's formulae can be expected to start at elevations of 10 degrees and to become somewhat onerous past 15 degrees elevation.
Gravity
We all understand gravity, I suppose. If it were the only force on a shell in flight, we'd see that shells fly in parabolic paths. A short range shot from a high-velocity gun will appear nearly flat, and progressively longer shots will require greater angles of elevation to loft the shell outward (as gravity tries to pull it back to earth), and the shells will land at negative angle at which they departed. Ballistics would certainly be easy if gravity were the only factor to consider, as for a given muzzle velocity and
Aerodynamic Drag
A shell moving at high speed through air meets frictional resistance, and it slows the shell down. As a consequence, the parabolic flight that you would have without drag becomes an assymmetric arc and shells fall back to earth more steeply than they departed.
Ballistic Drift
This section will be unduly long, as it touches on my own attempts to understand the magnitude and nature of this force which generally causes shells to "drift off" to the side as they fly downrange. Like any regular phenomenon influencing the fall of shot, it behooved a nation to develop and understand of drift's nature and to create mechanisms that might factor it out of the gunner's problem before he even gets called to action stations.
It is not easy to find comprehensible information on ballistic drift as a physical phenomenon. Indeed, it is hard to find specific data on a given weapon system for how far the shell would deviate laterally (generally to the right, given the customary direction of twist in rifling) as it traveled to various ranges. However, the 1918 Range Tables offer a little explanation for how the Royal Navy treated drift and some of the compiled range tables within include fairly complete drift data, although one might be suspicious as to which are experimentally obtained and which are the result of a mathematical model for drift.
It was observed that the length of the projectile was a primary factor for why different shells exhibited different drift behaviors[2], and a mathematical description of drift angles was derived for use in the form:
driftAngle = someConstantForThisGunAndProjectile * tangent(elevation)[3]
However, not all range tables within the volume have drift expressed in this manner, as determination of the constant for all guns was not possible before going to press.[4] The formula is puzzling, as it seems as though not only was a rule of thumb being entrusted to model drift for the world's pre-eminent navy, but that it had been recently conceived and relied upon empirical constants still being sorted out.
Critical thought indicates that the formula might not express the drift angles observed in test firings, but those allowances for drift provided by the Royal Navy's oft-employed mechanical drift correction built into many of her gun sight apparatuses wherein the sightsetting gear and scopes were simply cocked to the side a smidge so that as the gun was elevated a deflection was progressively induced. It is not clear, then, whether the drift data in the volume are results taken from this formula and why range tables did not include drift data based on a few test firings at different ranges and with other values plugged in after interpolating their likely best values.
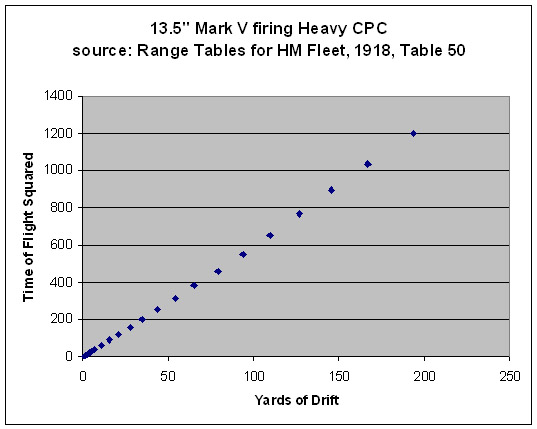
Ignoring for the moment our doubts as to where these data came from, a graphical analysis of the drift data from one range table (Table 50) does not seem to imply that it was spat out by the RN's drift angle formula. One caveat is that the first few data are likely distorted due to rounding errors, as the first 5 appear with only a single significant digit. This first scatter plot explores the correlation between the RN's formula and the data in the table.
The correlation seems fair, but a visual inspection clearly indicates a relatively weak relationship at the short range shots. Let us ignore the Royal Navy's best published thinking on the matter and work with a hypothesis that the lateral deviation observed in practice was the result of a constant force acting upon the shell throughout its flight, and that maybe the data in this one table are derived from actual test firings (possibly with some interpolation). This seems like a reach, but proves a gamble well worth taking: we achieve an even better fit, even when including the first 11 data points with their presumed rounding errors!
The conclusion is that extremely faithful simulation of drift can be attained by taking the most extreme (range, time-of-flight, drift) datum available for a gun/charge/projectile system and calculating a constant lateral force which, if applied continually during flight that produces the drift behavior observed in this single historical firing. A big win for the anal retentive game coder who lacks a PhD in Physics.
Footnotes
- ↑ "... it is unlikely that the results obtained at practice will differ widely from the range tables, and should a large error appear to exist it is generally advisable to seek the cause elsewhere than in the tables."
Range Tables for HM Fleet, Volume I, 1918, p. 5 - ↑ Range Tables for HM Fleet, Volume I, 1918, pp. 7-8
- ↑ Formula adopted vide Gunnery Order No. 200/1916
Range Tables for HM Fleet, Volume I, 1918, p. 8 - ↑ Range Tables for HM Fleet, Volume I, 1918, p. 8
Bibliography